Polygon Triangulation
My Role
~ Lead Developer (MSc Final Project)
Developed a Django web app to implement and visualize polygon triangulation. Built custom algorithms for vertex classification, regularization, and triangulation with an interactive D3.js frontend.
Timeline
~ 4 Months
(June 2024 - September 2024)
Impact
Contributed to the research and practical exploration of triangulation algorithms. The web-based platform designed to test edge cases and visualize results in real time helped bridge the gap between theoretical models and practical implementations, made these algorithms more accessible for future research and education.
About this Project
This MSc dissertation project focused on the practical implementation and visualization of simple polygon triangulation, a core problem in computational geometry with applications in computer graphics, GIS, and numerical analysis. I implemented a full triangulation pipeline using the Sweep Line Algorithm for vertex classification, regularization to split polygons into monotone parts, and a Doubly Connected Edge List (DCEL) for efficient polygon handling, before applying a custom triangulation algorithm. To make the process interactive, I built a Django-based web application with a D3.js frontend, enabling users to draw or input polygons and visualize each step—classification, regularization, and triangulation—in real time. The platform was tested with multiple datasets, achieving strong accuracy and revealing insights into challenging edge cases, ultimately bridging the gap between theoretical algorithms from Discrete & Computational Geometry and their practical, research-driven applications.Objective
The objective of this project was to design a practical implementation and visualisation solution for simple polygon triangulation through a combination of algorithmic development and an interactive web-based platform. The aim was to bridge the gap between theoretical approaches in computational geometry and their real-world applicability, creating a tool that supports testing, visualization, and research into triangulation algorithms.What really is Polygon Triangulation
Polygon triangulation is the process of dividing a polygon into a set of non-overlapping triangles whose union exactly covers the original polygon. This technique is widely used in computer graphics, computational geometry, and mesh generation to simplify complex shapes for further processing. The following outlines the step-by-step process used to achieve triangulation:- Check for x- or y-monotonicity: Determine whether the polygon is monotone along the x or y axis.

- Regularise the polygon into two or more monotone polygons: Insert diagonals to split the polygon into monotone sub-polygons.

- Triangulate the regularised polygon: Apply triangulation to each monotone sub-polygon.

Design and Developments
Implementation
The implemented process to triangulate a simple polygon was followed with the steps given as such. Each step prepares the data for the next, moving from raw coordinates to an interactive, visual triangulation result.
- Input: Parse user-provided coordinates (ordered vertex list) and validate that they form a simple polygon (no self-intersections).
- Classification of vertices: Use a sweep-line procedure to label each vertex (Start, End, Split, Merge, Regular) based on its local geometry and ordering.
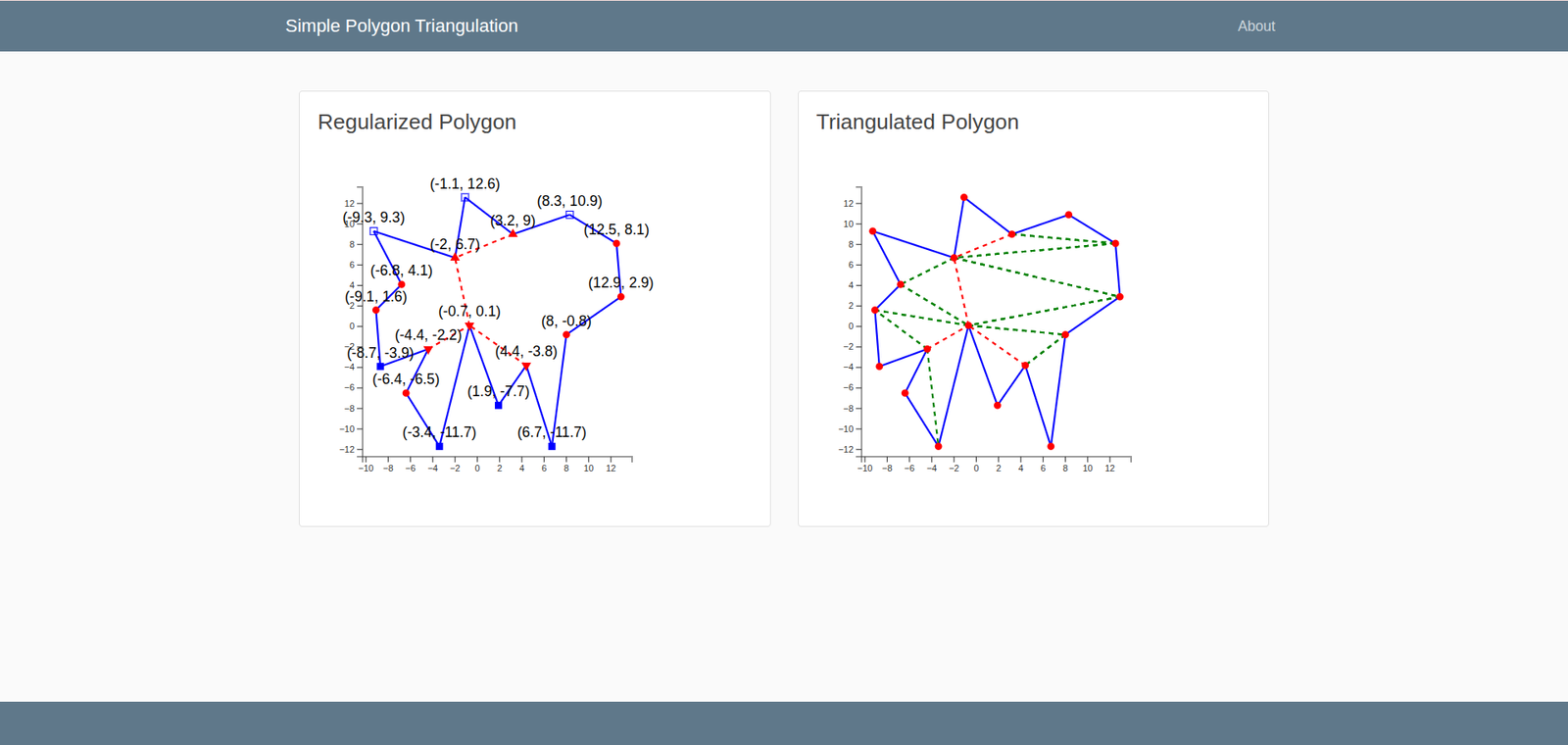
- Regularization: Insert diagonals guided by the classifications to decompose the polygon into one or more y-monotone sub-polygons. If none are needed, the polygon is already monotone.
- DCEL Construction: Build a Doubly Connected Edge List to represent vertices, half-edges, and faces, enabling efficient traversal of the monotone regions created during regularization.
- Triangulation: For each monotone region, sort vertices by descending y (breaking ties by x), then apply a stack-based method to add non-intersecting diagonals and form triangles. If no DCEL was required, triangulate the original polygon directly.
- Result the triangulated figure: Store and render the outputs—classified vertices, regularization diagonals, and final triangle edges—so the complete triangulation is visualized.

The 6 step approach was sub-divided into 4 steps to make it more easier to move forward, which is given as follows:
-
1. Input and preprocessing: Defining the edges of the polygon based on the given coordinates.

-
2. Vertex classification and plotting: Classifying vertices and plotting them accordingly.


-
3. Regularisation: Simplifying the polygon into monotone sub-polygons where necessary.

-
4. Creation of DCEL and Triangulation: Constructing the DCEL structure and generating the final triangulation.


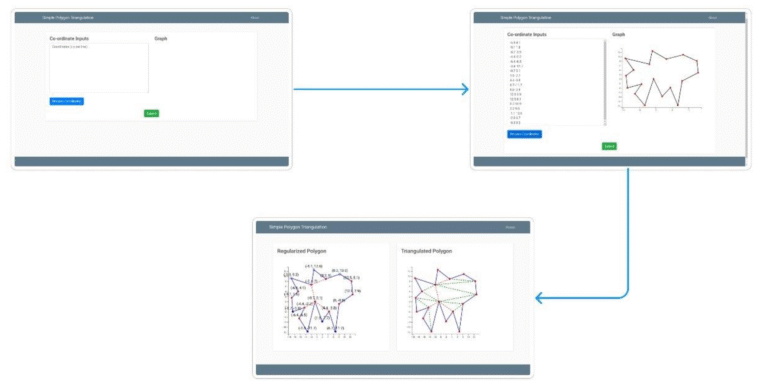
UI/UX Mockup

Actual Webapp Based on the UI/UX Mockup
Tools & Platforms Used
Geogebra (Dynamic mathematics software)
Deployment and Hosting
The application is deployed on an AWS EC2 Ubuntu server using a full production-ready setup with Gunicorn and Nginx. Gunicorn handles the Python WSGI execution, while Nginx acts as a reverse proxy and serves static files to ensure high performance. The site is configured with a custom domain and secured using HTTPS through Let’s Encrypt and Certbot, which also manages automatic SSL renewal. All project updates are pushed from the local development environment to GitHub and then pulled onto the server as part of a simple, efficient deployment workflow. This setup closely reflects real-world production environments, ensuring the application runs smoothly, securely, and reliably.Other tools :
Timeline of the project
