Solving Travelling Salesman problem using Parallel and Distributed programming through OpenMP and MPI
My Role
~ Developer
Devised structured scripts to implement parallel and distributed solutions for the Traveling Salesman Problem, leveraging the Barkla server’s high-performance computing resources.
Timeline
~ 3.5 Months
(October 2023 - January 2024)
Impact
Demonstrated the effectiveness of parallel and distributed computing for solving the Traveling Salesman Problem, achieving faster execution on large datasets and showcasing the potential of HPC resources like the Barkla server for real-world optimization tasks.
About the Project
This project was part of my MSc coursework in parallel and distributed computing, where I explored solutions to the Traveling Salesman Problem (TSP)—a classic NP-hard optimization problem with applications in logistics, routing, and network design. The work focused on designing and implementing structured scripts that leveraged OpenMP for parallel programming and MPI for distributed execution. By running experiments on the Barkla high-performance computing (HPC) cluster, I evaluated scalability and performance across datasets of varying sizes. The project demonstrated how computationally intensive problems can be optimized through parallelization, highlighting the efficiency gains of utilizing HPC infrastructure for real-world problem solving.
The objective of this project was to design and implement efficient solutions for the
Traveling Salesman Problem (TSP) using parallel and distributed computing techniques.
By applying OpenMP and MPI to optimize execution across multiple cores and nodes on the
Barkla high-performance computing (HPC) cluster, the project aimed to evaluate scalability,
improve performance on larger datasets, and demonstrate how high-performance computing can make
traditionally intractable problems more feasible in real-world applications.
Objective
Developments of scripts
Files Included in the github repository :
-
- coordReader.c: includes fucntions that read the coordinate input from a file, and write the final tour to a file.
- 9_coords.coord, 16_coords.coord and 512_coords.coord: co-ordinate files.
- 9_cout.dat, 9_fout.dat, 9_nout.dat, 16_cout.dat, ... : expected output files from the three methods(cInsertion, fInsertion, and nAddition).
- Continuous Assessment files 1 and 2: files including outline of the parallelism and distribution of methods.
- ompcInsertion.c, ompfInsertion.c, ompnAddition.c: parallelised versions of methods implemented in c.
- main-openmp-only.c: sequential implementation of all three methods to give out the best tour starting from one co-cordinate only.
- main-mpi.c: distributed implementation of the parallelised program running those methods on multiple instances through multiple nodes.
- Makefile: compiles all versions of c and makes them into executables to be ran in terminals.
- MPI_batch.sh: bash script to submit jobs on Barkla server(in this case, University of Liverpool's Server) through slurm.
- Output folder: consists of output files given through the bash script which shows the execution of programs on different coordinates and there execution time and the number of threads used.
Nearest Addition Approach to parallelization
-
We start by initializing a parallel region within which the nearest addition will be implemented. As we have
to find the nearest unvisited vertex with the edge joining those vertices having the lowest cost, this part
within the parallel region is handled by a parallel block carrying out the process using a single thread. Now
that the nearest node has been discovered the next thing is to add this node before or after the previous node
depending upon whichever tour has the lower cost, this makes two separate tours and compares them which
is also done by the same parallel region. As we go on, the nodes in visited nodes array are marked to be
visited and the tour length increases until all coordinates are visited. The tour cost is compared between
nodes and then updated at the end which is carried by another parallel region using #parallel omp
collapse(2) directive. This value later is utilized for finding out the best tour amongst all the other instances
of tours starting from different nodes. This approach optimally leverages parallel processing capabilities of
the program.
main-openmp-only.c
-
The serial solution to distribution implementation is stated in this file which finds out the best tour amongst all the tours of ompcInsertion.c ompfInsertion.c and ompnAddition.c by running all its instances in sequential manner. The output tours are then outputted in their respective text files. The formation of distance matrix is done using a parallel block.
main-mpi.c
-
// strategy for parallel solution of distributed implementation
Firstly, MPI environment is initialized which involves obtaining the total number of MPI processes and rank of the current MPI process. The root process continues and goes on to readthe coordinates from input files after which the program proceeds to create tour arrays and the necessary variables that are going to be used. Moving further the separate tours of all algorithms are calculated across all instances and the tour arrays are updates based on the finding the lowest possible tour. The distance matrix again is computed in using a parallel region. The final tours are then outputted in their respective text files.
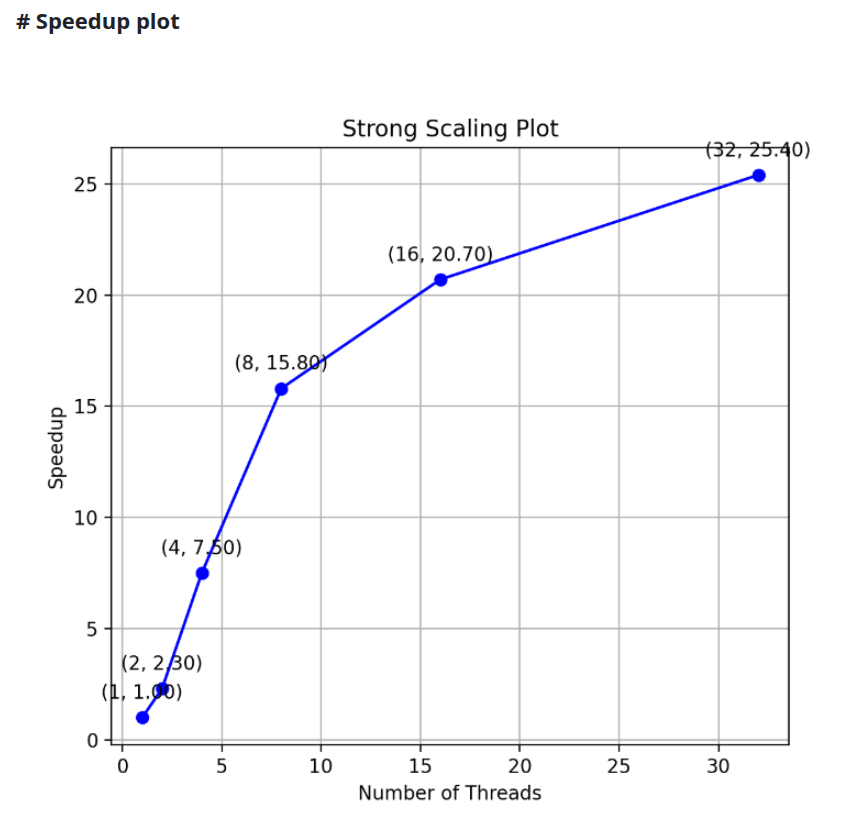
Speedup Plot
-
For generating the speedup plot the final program has been executed over the large dataset of 512
coordinates over one MPI process for variable OpenMP threads from 1-32. The plot looks as follows:
Parallel Efficiency Plot
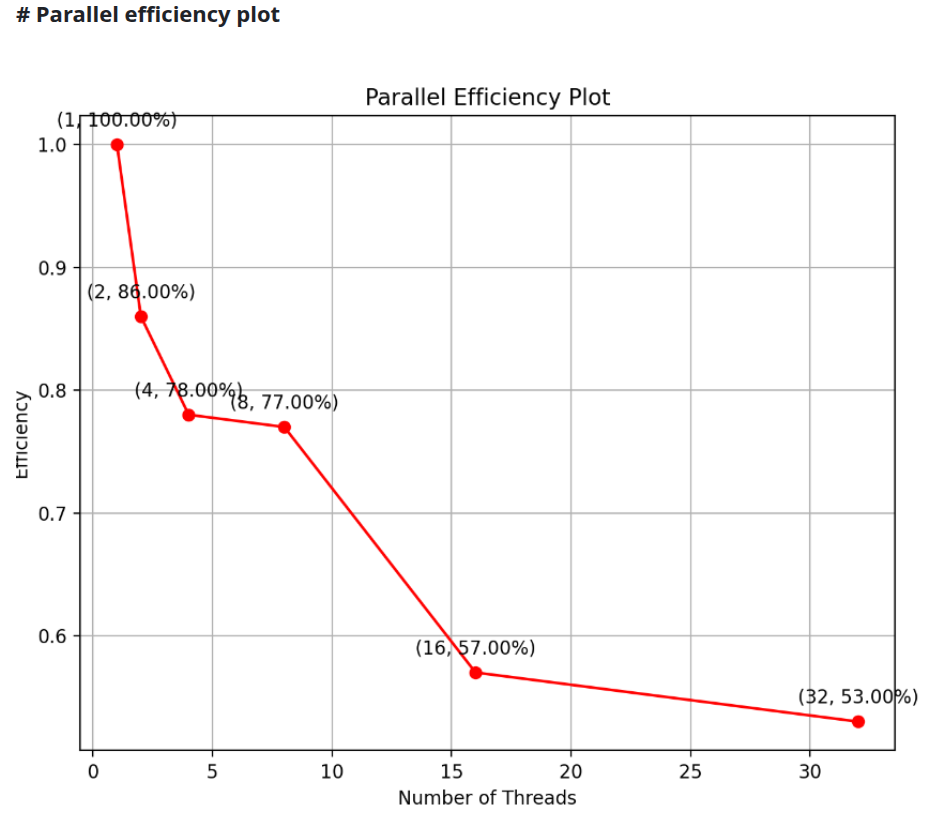
-
By dividing the speedup from number of threads used for that speedup we get the required parallel efficiency of that datapoint in percentage, this contributes to the formation of parallel efficiency plot which
is as follows:
-
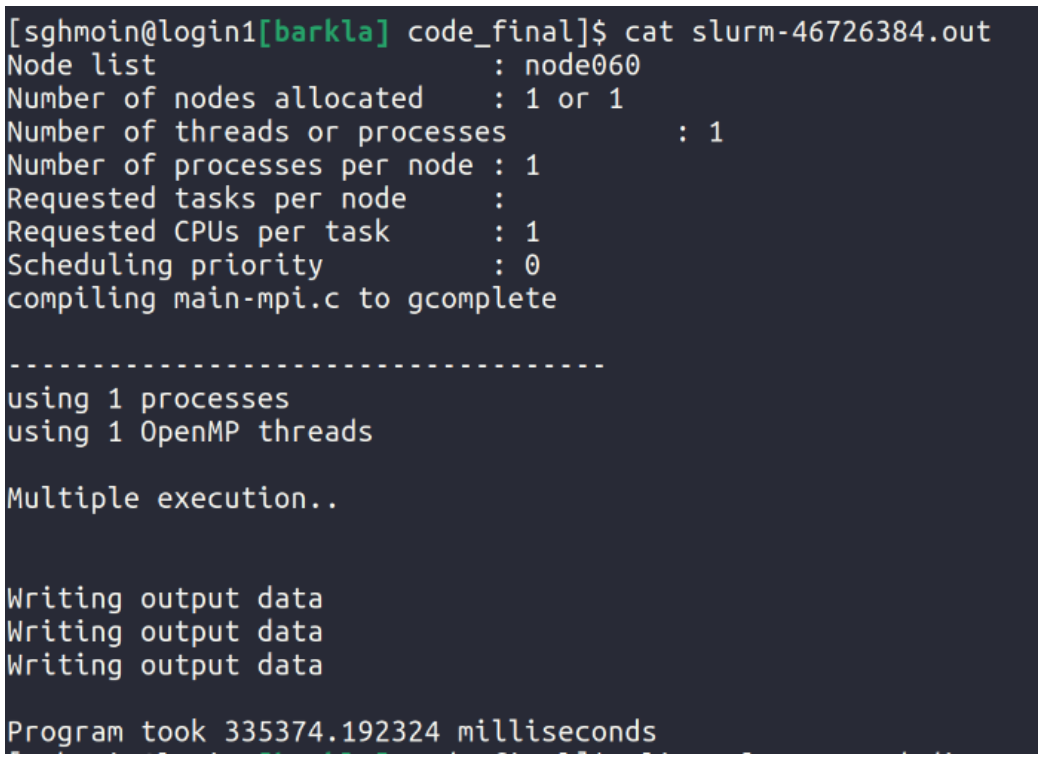
// Screenshots of execution and sample slurm output are as follows:

Tools Used :
Project Summary
This project focused on solving the Traveling Salesman Problem (TSP) using parallel and distributed programming techniques. By implementing solutions with OpenMP and MPI on the Barkla high-performance computing (HPC) cluster, I evaluated performance across datasets of different sizes and showed how parallelization significantly improves efficiency for computationally intensive problems. The work highlights the practical value of high-performance computing in tackling large-scale optimization challenges in logistics, routing, and network design.